Se si confronta il testo di Pacioli con le 60 tavole che chiudono la Divina proportione si nota subito che c’è una differenza sostanziale tra la costruzione dei solidi indicata nel testo e la realizzazione delle “supreme et legiadrissime figure de tutti li platonici et mathematici regulari et dependenti, ch’in prospectivo disegno non è possibile al mondo farle meglio”. Pacioli, infatti, segue le procedure grafiche riscontrabili nell’edizione a stampa dell’Euclide di Ratdolt del 1482  e finalizzate alla dimostrazione matematica. Le figure dei solidi, “facte et formate per quella ineffabile senistra mano, a tutte le discipline mathematici acomodatissima del principe oggi fra’ mortali, Lionardo nostro da Venci”, si presentano invece in una configurazione spaziale prospettica che accentua le tre dimensioni dei corpi regolari al fine di visualizzarli come oggetti materiali. L’aggiunta del colore contribuisce a rendere concreta la realtà dei poliedri e pertanto a ragione Pacioli si vanta di presentare agli occhi di Ludovico il Moro “forme ali viventi fin hora ascoste”.

Ycocedron planus solidus

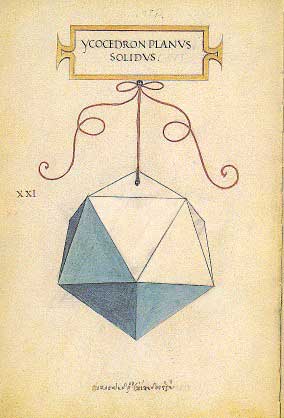Icosaedro (20 triangoli) piano solido

Come ha ben rilevato Marisa Dalai Emiliani, l’idea peculiare e qualificante della visualizzazione di Leonardo è quella di rappresentare non astratte entità concettuali ma corpi solidi, dotati di concretezza volumetrica (si pensi a tutte le tavole in cui il poliedro è definito “solidus”) oppure realizzati mediante una semplice struttura-telaio, essenziale ma ben connessa come certamente lo erano i modelli lignei fabbricati da Pacioli (ed è il caso di tutte le tavole in cui il poliedro è presentato invece come “vacuus”). Questa scelta certo concorde di Pacioli e Leonardo per la corporeità, la fisicità dei modelli costruiti è testimoniata, mi sembra, dal modo genialissimo con cui l’artista ha voluto mostrare i solidi, non appoggiati semplicemente su una superficie piana, né levitanti nello spazio astratto che la pagina bianca suggerisce con la sua bidimensionalità, ma al contrario sospesi mediante un complesso e sempre variato sistema di piccoli anelli e di nodi, tramite un cordoncino che si avvolge su se stesso per il peso che deve sostenere, fissato al centro delle cartelle ansate in cui leggiamo i nomi latini dei poliedri  (M. Dalai Emiliani, Raffaello e i poliedri platonici, in Studi su Raffaello…cit., pp. 93-109, p. 101).

L’attenzione alla corporeità e fisicità dei corpi regolari è testimoniata dalla costruzione da parte dello stesso frate Luca di modellini in legno dei poliedri, presentati prima al Cardinale Giuliano della Rovere nel 1489,  poi a Ludovico il Moro, e infine alla Signoria di Firenze sotto il governo del Soderini. Le tavole di Leonardo, pertanto, costituiscono l’equivalente grafico delle sculture lignee di Pacioli e portano a compimento quel processo di visualizzazione della geometria euclidea, che cominciato con il Trattato d’abaco di Piero della Francesca, conduce le “forme astratte” dei solidi platonici ad incarnarsi in concrete “forme materiali”, scolpite nel legno o disegnate in prospettiva.

 La corrispondenza tra il testo matematico e le tavole disegnate da Leonardo sembra essere essenziale per Pacioli; per questa ragione, “a più piena intelligentia  de questo nostro compendio, per saper retrovare tutte le proprie figure in prospectivo aspecto in questo sequente poste, e ancho le materiali, secondo lor publica tavola”, il frate spiega a Ludovico il Moro come riferire i numeri romani disseminati nel testo alle tavole che chiudono l’opera.

E quel medesimo numero – chiarisce Pacioli – aponto farete de trovare de sotto dove in questo dicti corpi sonno per ordine tutti figurati. El qual numero similmente in quel luogho in margine sirà posto…E quella tal figura sirà del dicto corpo facto in piano con tutta perfectione de prospectiva, commo fa el nostro Lionardo Vinci. E questi medesimi numeri anchora recercarete fra le forme materiali de dicti corpi dependenti con lor nome in greco e in latino, posti in un breve sopra ciascuno, afixo nel suo cordiglio, fra doi ambre negre, pur referendo ognuno commo è dicto al numero posto in margine dove di quel se tracta. E V. Celsitudine a l’uno e al’altro modo harà loro dispositioni, le quali non de vil materia (commo per inopia a me è stato forza) ma de prezioso metallo e fine gemme meriterieno essere ornati.

Dueocedron planus solidus

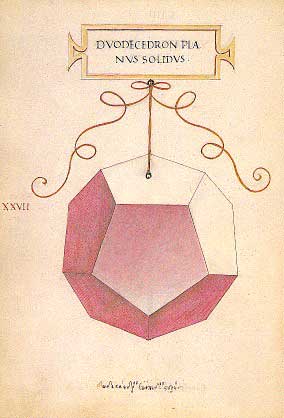Dodecaedro (12 pentagoni) piano solido

La descrizione di Pacioli non può essere più chiara: le tavole disegnate “con tutta perfectione de prospectiva” da Leonardo si riferiscono alle “forme materiali” descritte nel testo e costruite in legno. Disegno, scultura lignea e dimostrazione matematica si integrano a vicenda al fine di “incarnare” i corpi geometrici di Euclide in oggetti concreti, “ciascuno afixo nel suo cordiglio” quasi ad evidenziarne il peso e la solidità.

La stessa impressione di concretezza dei corpi regolari  si ha dal ritratto di Luca Pacioli conservato a Napoli presso il Museo di Capodimonte, dove il testo degli Elementi, aperto su una pagina  del libro XIII, è affiancato da un dodecaedro ligneo appoggiato sopra la Summa. In questo ritratto del frate sono presenti tutte le operazioni necessarie a trasformare gli oggetti astratti descritti nel testo in oggetti concreti tridimensionali: la proposizione degli Elementi, indicata dalla mano sinistra di Pacioli, riceve una prima visualizzazione grafica nella lavagna a destra del frate, sul bordo della quale è inciso il nome “Euclides”. La successiva operazione del passaggio dall’astratto al concreto è simbolicamente rappresentata da due solidi: il dodecaedro ligneo posto alla sinistra del frate e il corpo di 26 basi, appeso per un filo, come i solidi delle tavole di Leonardo.

Il rombicubottaedro, colmo a metà d’acqua,  rifrange per tre volte, sulla sua superficie di cristallo, il Palazzo Ducale di Urbino. Il virtuosismo ottico con il quale l’autore del ritratto raffigura il palazzo di Urbino rimanda al personaggio che affianca Pacioli, e che sembra si possa identificare nel giovane Guidubaldo da Montefeltro, al quale il frate dedica la Summa. Com’è noto, Bernardino Baldi alla fine del XVI secolo, nelle sue Vite de’ matematici, riferiva di un’opera di Piero della Francesca, conservata “nela guardarobba de’ nostri serenissimi Principi di Urbino”, raffigurante il “ritratto al naturale d’esso frate Luca, col suo libro avanti dela Somma Aritmetica et alcuni corpi regolari finti di cristallo appesi in alto, ne’ quali e da le linee, e da’ lumi e da le ombre si scopre quanto Piero fosse intendente ne la sua professione”.

  Quale che sia la relazione fra la descrizione del Baldi e l’opera conservata a Napoli, resta comunque evidente l’associazione tra frate Luca e le “forme materiali” dei poliedri regolari. A questo argomento, infatti, Pacioli dedicò gran parte delle sue ricerche e dei suoi studi dopo la stesura della Summa e l’incontro con Leonardo, alla corte di Ludovico il Moro, costituì senza dubbio l’occasione più proficua per realizzare un progetto grafico al quale il frate non poteva dare seguito senza l’aiuto di un  pittore abile nella prospettiva. Chi meglio di “quella ineffabile senistra mano, a tutte le discipline mathematici acomodatissima,” poteva disegnare le tavole della Divina proportione?

Leonardo, che nel dipingere appariva agli occhi di Pacioli come il “principe oggi fra’ mortali”, era sicuramente nel campo della visualizzazione dei poliedri il degno erede di Piero della Francesca, il “monarca” della pittura, come lo aveva definito frate Luca nella Summa. Leonardo, infatti, realizzò tavole dei poliedri tali “ch’in prospectivo disegno – come notò lo stesso autore della Divina proportione - non è possibile al mondo farle meglio”. La collaborazione fra il matematico e il pittore avveniva tramite il libro di Euclide, che il primo traduceva in volgare ad uso del suo “conterraneo” toscano.

Gli studi di Augusto Marinoni sulla matematica di Leonardo hanno dimostrato inequivocabilmente come prima dell’incontro con Pacioli le conoscenze aritmetiche e geometriche del pittore fossero molto limitate e approssimative (A. Marinoni, La matematica di Leonardo, Milano 1982). L’arrivo a Milano di frate Luca dal Borgo coincise, invece, con un processo di acculturazione matematica di Leonardo, riscontrabile nei codici Forster II (1°), Madrid II, e nei manoscritti M, I, L  e K (I e II) dell’Institut de France, databili nel periodo di frequentazione dei due toscani. L’analisi attenta e puntuale degli scritti matematici contenuti nei suddetti taccuini leonardeschi conduce Marinoni a questa conclusione:

Dal 1496 fino al 1504 circa Leonardo è in contatto continuo o saltuario, diretto o indiretto (tramite i libri di maestro Luca) col Pacioli. In questi anni si accende e sviluppa il suo amore per la geometria che si esplica sia nei disegni per la Divina proportione sia nello studio sistematico di Euclide, chiaramente dimostrabile per i primi sei libri e parte del decimo. La presenza di quest’ultimo fin dalle prime “lezioni” significa che Leonardo affrontò subito il problema dei numeri irrazionali, ovvero il rapporto tra segmenti fra loro incommensurabili, quali il lato e la diagonale del quadrato, il raggio e la circonferenza e il problema della cosiddette “radici sorde”. In questa fervida iniziazione di Leonardo ai problemi  della geometria non dovrebbe porsi in dubbio la posizione del Pacioli, quale ispiratore, consigliere, maestro e traduttore. Tra l’omo sanza lettere e il difficile latino degli Elementi era indispensabile la mediazione di un letterato matematico quale era l’amico e, come amava chiamarsi maestro Luca, compatriota.

Albero delle proporzioni nel codice Madrid II di Leonardo (c. 78r) e nella Summa del Pacioli

La relazione di frate Luca con Leonardo è un tipico caso di convergenza degli interessi della matematica dotta con la cultura dei pratici. Leonardo, che compra la Summa per 119 soldi (Atl 228r, già 104r.) e annota: “Impara la multiplicatione de le radici da maestro Luca” (Atl.331r, già 120r), è un allievo ideale per Pacioli. Al pittore, ormai quarantenne, frate Luca può insegnare il fondamento di tutte le arti e di tutto lo scibile: la teoria delle proporzioni.

Come abbiamo più volte rilevato, la dottrina delle proporzioni è il nucleo del programma di matematizzazione del sapere perseguito da frate Luca. Leonardo dovette essere particolarmente interessato a questa dottrina, che si ritrova in maniera non trascurabile in almeno tre codici: il Madrid II, il Forser II (1°)  e il ms. K dell’Institut de France. Il manoscritto Madrid II (ms.8936), contiene da f. 46v a f.50r, un riassunto della sesta distinzione della Summa, dedicato alle proporzioni e alla proporzionalità. Lo stesso albero di c. 78r, presente in questo codice, ricalca l’arbor proportionis et proportionalitatis contenuto nell’opera di frate Luca. Il codice Forster II (1°), dal f. 14r a 22r contiene appunti sulla teoria delle proporzioni che riconducono alla Summa. Nel manoscritto K, infine, costellato di numerosi riferimenti alle proposizioni degli Elementi di Euclide, si legge (f.49r) : “La proporzione non solamente nelli numeri e misure fia ritrovata, ma etiam nelli suoni, pesi, et tempi e siti e qualunque potenzia si sia”. La frase, che testimonia l’universalità dell’applicazione della teoria contenuta nel quinto libro degli Elementi, viene copiata parola per parola dalla Summa. Pacioli, a sua volta, la traduce dal commento del Campano all’opera di Euclide.