Natura omniparens produxit corpora quinque. / Simplicia haec certo nomine dicta manent./ Composito in numerum concurrunt addita quinque / Atque inter se consociata vigent / Condita principio pura et sine labe fuere / Nomina sunt aer, coelum aqua flama et humus / Foetibus innumeris voluit Plato maximus illa / Esset ubi est primum sumpta figura: dare / Sed quia naturae lex nil concedit inane / (In coelo et mundo dixit Aristoteles) / Quodque unum per se positum est: caret atque figura / Nulla subest oculi supposito species / Propterea Euclidae sublimius atque Platonis  / Ingenium excussit sphaerica quinque alia / Iocundi aspectu et multum irritantia sensum / Monstravere bases ut latus omne docet.

  Con questo epigramma dell’umanista e cultore di matematiche Daniele Gaetani, liberamente tradotto in volgare dallo stesso Pacioli e stampato a fronte dell’originale in latino, si apre l’edizione a stampa della Divina proportione del 1509. La commistione fra cosmologia platonica e geometria euclidea è fin troppo palese. Gli Elementi di Euclide sono considerati come un approfondimento scientifico della concezione del mondo e dell’origine dei 5 elementi contenuta nel Timeo. Sulla scia della chiave di lettura proposta da Gaetani frate Luca si accinge a volgarizzare gli ultimi libri dell’opera euclidea. Il filo conduttore dell’opera è costituito dai solidi platonici. È quindi opportuno ora entrare nel merito di questa sorta di “analisi cristallografica” del reale, compiuta da Pacioli e di specificare in che modo sono costruiti i poliedri regolari. Essi, altrimenti detti sferoidi - perché inscrivibili in una sfera -, sono composti da superfici regolari.

Onde – precisa frate Luca - li decti sonno chiamati regulari perché sonno de lati e anguli e basi equali, e l’uno dal’altro aponto se contiene, commo se mostrarà, e conrespondono ali 5 corpi semplici in natura, cioè: terra, aqua, aire, fuoco, e quinta essentia, cioè virtù celeste che tutti gli altri sustenta in suo essere. E sì commo questi 5 semplici sonno bastanti e sufficienti in natura, - altramente seria arguire Idio superfluo o vero diminuto al bisogno naturale; la qualcosa è absurda, commo afferma el philosopho che Idio e la natura non opera invano, cioè non manca al bisogno e non excede quello –; così, a simili, le forme de questi 5 corpi, deli quali s’à a dire, aponto sonno 5, ad decorem universi, e non possano esser più per quel che sequirà. E però non inmeritamente, […], l’antico Platone nel suo Thymeo le figure de dicti regulari atribuì ali 5 corpi semplici, commo in la 5ª convenientia del divin nome ala nostra proportione atribuita de sopra fo detto.

L’idea che si profila in questo passaggio della divina proportione è che la natura sia composta da 5 elementi “bastanti e sufficienti” a render conto di tutto il creato e scelti da Dio secondo un principio di economia, che consente di soddisfare “al bisogno naturale” nel migliore dei modi possibili,  in maniera tale che – per dirla con frate Luca -“non manca al bisogno e non excede quello”. Il motivo per il quale Dio, per creare il mondo naturale, sceglie soltanto 5 elementi risiede nella dimostrazione geometrica che i poliedri regolari sono soltanto cinque. La necessità fisica che gli elementi naturali siano 5 è pertanto analoga alla necessità logica che i poliedri regolari siano soltanto i cinque indicati da Platone nel Timeo. Non esistono altri poliedri regolari oltre il tetraedro, l’ottaedro, il cubo, l’icosaedro e il dodecaedro; così come non esistono altri elementi semplici in natura, oltre il fuoco, l’aria, la terra, l’acqua e la quinta essenza. La necessità che i poliedri siano soltanto 5 è dimostrata dalla geometria euclidea. Un angolo solido - dice infatti Pacioli - deve essere costituito da tre “anguli superficiali”, e, per qualsiasi figura piana usata per formare gli angoli solidi, è sempre minore di quattro angoli retti, “commo testifica la 21ª del 11°” degli Elementi. Un angolo solido, quindi, non può essere formato da superfici esagonali, o da poligoni con un numero di lati maggiore di cinque, dato che in questo caso tre angoli piani supererebbero 360 gradi. Restano utilizzabili perciò soltanto il pentagono regolare, il quadrato e il triangolo equilatero. Pacioli mostra nel XXV capitolo che con il pentagono è possibile costruire soltanto un poliedro regolare, e cioè il dodecaedro, con il quadrato soltanto il cubo, e con il triangolo equilatero solo ed esclusivamente gli altri tre sferoidi.

L’impossibilità geometrica di costruire un sesto poliedro regolare corrobora - secondo frate Luca - la tesi per la quale in natura non ci sono più di cinque elementi a costituire la struttura originaria del mondo.

Una volta stabilito quanti e quali siano i poliedri regolari e, dimostrato che non possono essere più di cinque, Pacioli procede ad esaminarli uno ad uno, precisando sia il modo di costruirli sia le proporzioni fra i lati dei poliedri e il diametro della sfera nella quale sono inscritti. La trattazione matematica dei capitoli XXVI-XXX del Compendium de divina proportione ha delle caratteristiche di stile che la distinguono sia dalla forma deduttiva degli Elementi, sia dalla numerizzazione dell’opera di Euclide presente nel Libellus de quinque corporibus regularibus che chiude l’edizione a stampa del 1509. Del testo euclideo Pacioli si limita a riportare il procedimento di costruzione delle figure e l’indicazione della proposizione degli Elementi dalla quale dipende la realizzazione grafica. D’altra parte nemmeno si può inserire a pieno titolo la Divina proportione nell’ambito della tradizione abachistica poiché non contiene le trascrizioni numeriche del testo euclideo e le applicazioni pratiche nella soluzione di problemi, tipiche invece del Particularis tractatus de quinque corporibus regularibus che compare a conclusione della Summa. Quella che disegna Pacioli nella Divina proportione è una geometria euclidea di divulgazione, destinata più ad un uso artistico, o anche filosofico, che pratico-tecnico.

Pacioli volgarizza il XIII libro degli Elementi seguendo uno stile espositivo ben preciso: ogni proposizione euclidea è tradotta soltanto per la parte che enuncia il teorema e descrive la costruzione della figura; la dimostrazione viene in molti casi omessa; infine, si specifica sempre alla fine di ogni capitolo la proporzione che sussiste tra il diametro della sfera ed il poliedro in essa inscritto. Le proporzioni costituiscono, infatti, il filo rosso della trattazione pacioliana. Ricapitolando i rapporti fra il diametro della sfera e i lati dei poliedri inscritti frate Luca ricorda che per il tetraedro la proporzione è sesquialtera (3:2), per il cubo tripla (3:1), per l’ottaedro doppia (2:1). Per quanto concerne, invece, l’icosaedro e il dodecaedro, la proporzione è irrazionale, dal momento che in entrambi i casi il rapporto fra il diametro e lo spigolo fornisce, a causa della divina proporzione, quantità “incommunicabili”, e precisamente una “linea minore” per l’icosaedro e un “residuo” per il dodecaedro.

Nel capitolo XXIX, dedicato all’icosaedro, Pacioli, anziché limitarsi a rimandare il lettore agli Elementi, fornisce, oltre alla procedura di costruzione, anche la dimostrazione che il poliedro di 20 basi triangolari così formato è inscrivibile in una sfera.

La stessa trattazione deduttiva è riservata al dodecaedro. La 17ª proposizione del XIII libro degli Elementi, è infatti, tradotta integralmente in volgare. Il motivo per cui Pacioli si dilunga per gli ultimi due poliedri a riportare anche le dimostrazioni geometriche è principalmente connesso all’impiego della divina proportione nella loro costruzione. A prescindere dagli addentellati teologici della “proportione havente el mezzo e doi extremi” appare tuttavia evidente che frate Luca tende a condurre il lettore verso l’idea che l’ordine dei corpi regolari sia strettamente connesso alle proporzioni costanti che li costituiscono.

L’ultima proposizione del XIII libro degli Elementi, è a questo proposito, significativa. Pacioli, anche in questo caso, riporta la traduzione completa in volgare del testo di Euclide al fine di dimostrare come i rapporti reciproci fra poliedri siano riconducibili alle proporzioni che legano gli spigoli dei 5 corpi regolari con il diametro della sfera nella quale essi sono inscritti. 

Dopo aver condotto a termine la dimostrazione Luca dal Borgo conclude :

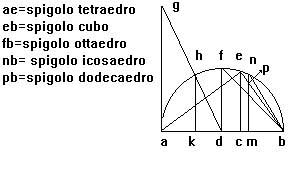
Sonno adoncha trovati li lati de li 5 corpi premessi, o voi dir anteposti, mediante il diametro de la sphera solamente a noi proposto; li quali lati sonno questi: cioè ae de la pyramide de 4 basi[tetraedro], eb lato del cubo; fb lato del 8 basi [ottaedro]; e lo nb lato del 20 basi [icosaedro]; e la linea pb lato del dodici basi [dodecaedro].

Considerando le proporzioni che intercorrono tra le misure degli spigoli dei poliedri, frate Luca rileva come esse “quasi con quel medesimo ordine che fra loro se sequitano, con quello fra loro excedino”. L’ordine tra le misure degli spigoli è il seguente: ae (lato tetraedro) > fb (lato ottaedro) > eb (lato cubo) > nb (lato icosaedro) > pb (lato dodecaedro). 

Onde apare li lati deli 5 corpi antedicti quasi con quel medesimo ordine fra loro se sequitano con quello fra loro se excedino. Solamente questo ha la instantia: cioè non se observa tal ordine nel cubo e nell’octocedron, cioè in lo 8 basi. Pero chel lato delo 8 basi antecede al lato del cubo, avenga chel cubo anteceda all’octocedron in fabrica e formatione, commo nel 13° apare e non è senza misterio. Onde in la formatione el cubo se pone al’octocedron perché per la medesima divisione del diametro dela sphera proposta, se trova el lato dela piramide de 4 basi triangolari e lo lato del cubo.

Le proporzioni non soltanto costituiscono il principio generativo dei poliedri ma anche il loro principio d’ordine. Non a caso l’argomento centrale del rapporto intellettuale tra Pacioli e l’autore della tavole del suo libro, e cioè Leonardo, è costituito proprio dalla teoria della proporzioni.